Components
of Bethe-Bloch Theory
Components
of Bethe-Bloch TheoryThe various components of Bethe-Bloch theory are reviewed in "Stopping of Energetic Light Ions in Elemental Matter", J. F. Ziegler, Applied Physics Reviews / J. Applied Physics, 85, 1249-1272 (1999). This paper is included as an Acrobat PDF file (600 kB). (Download Paper) The basic equations for high energy ion stopping using the Bethe-Bloch theory are shown below (copied from the above paper).
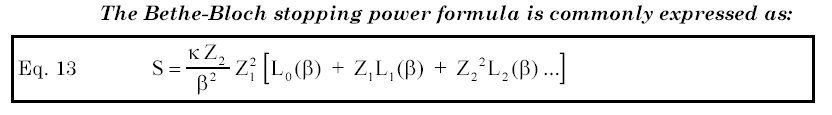
The pre-factor above evaluates the basic stopping between two particles of atomic number Z1 and Z2. This is followed by an expansion of terms based on powers of the ion's atomic number, Z1. The first term is the primary modification and is discussed below. The second term is the only term that includes an odd power of the ion's atomic number, Z1 (when combined with the Z12 of the pre-factor). It is often called the (Z1)3 term, or the "Barkas Effect" after the discovery that the stopping of positive particles is significantly different than for negative particles. The final term is called the "Bloch Effect" and is a minor correction..
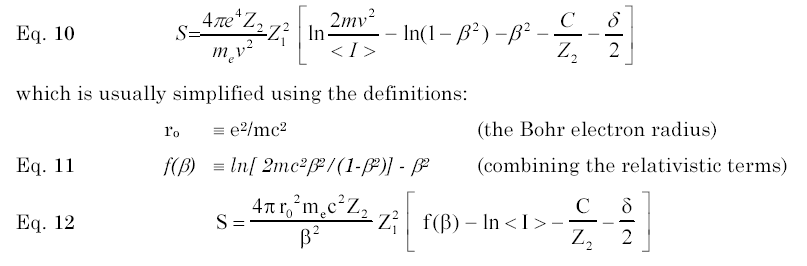
Eq. 10 shows the stopping equation with only the first factor of Eq. 13, L0(B), expanded into several terms. The terms within the square parenthesis are modifications based on the structure of atoms. Using the substitutions shown in Eq. 11, the equation can be reduced to the form of Eq. 12. In this final equation, the first term of the parenthesis collects all the relativistic corrections to stopping. The second term incorporates the target atom's atomic energy structure. The third term is called a Shell Correction, and corrects for the electron velocity distribution in the target. Finally, the fourth them is called the Density Correction and it corrects for the dielectric polarization of the target.
The plots below show the relative contribution of the various components for typical calculations of ion / target combinations.