(This review is taken from "The Stopping and Range of Ions in Matter")
The study of the penetration of a particle into matter might begin 400 years ago with the study of projectile ballistics, since the understanding of cannonballs in a viscous medium might be considered similar to the penetration of particles in matter.
A study was done by Leonardo DiVinci on catapults and how to increase the range of their projectiles (~1580). Unfortunately, his knowledge of dynamics was not as good as his analysis of static structures (levers, etc.) and he began with the unfortunate premise that the velocity of a projectile was proportional to the maximum force exerted on it, and hence what he actually derived was an early version of GIGO (Garbage In � Garbage Out). Other studies on catapults and projectiles were published by Galileo and Newton. But of special note was the analysis by a British vicar, Benjamin Robins, who attempted to help his Navy design better cannons during the Napoleonic Wars. His treatise, published in 1804, was called �New Principles of Gunnery� and reached the important conclusion that the energy loss of a projectile in a viscous medium was proportional to its velocity (see ref. 1804). This result was widely discussed and criticized, until Robins invented a ballistic pendulum apparatus to measure the effect. Since his result is similar to the quantum mechanical solution for the energy loss of charged particles in an electron gas, developed 130 years later, it is worth noting Robin�s major scientific contribution. Later, similar studies were published by Euler, LaPlace and Lavoisier, all of whom reached the same conclusion as Robins for low speed projectiles.
However we shall review only the last century, from the discovery of radioactive particles (1895) to the dawn of computer physics (1970). Scientific progress since 1970 is the subject of the remainder of this book. Certain terminology is traditional, and we shall use it from the beginning:
�� Ion = The moving atom, whether it is charged or neutral. Its atomic number is Z1, its mass is M1, its energy is E, and its velocity is E/M1. This velocity is only used to compare relative velocities, so the fact that it is squared is usually ignored.
�� Atom = Any target atom, with atomic number, Z2, and mass, M2.
�� Stopping Power = The rate of energy loss by the ion in the target, defined as dE/dx, the energy loss per unit distance, x. Some authors use stopping cross-sections, or inelastic losses or similar descriptions for the same concept. Recently, some authors have converted to using the phrase stopping force, which more aptly describes the units of energy loss per length of travel, but for this historical section we shall use the traditional phrases.
The development of the theory of an ion slowing in a solid has been difficult because the problem of describing both the ion and the target is complex. Once the ion penetrates a solid, it is quickly stripped of some of its electrons, and its charge state becomes a function of the target. The target feels the ion coming, and its electrons polarize around the moving ion. The charge state of the ion is modified by the polarized target, which then further affects the target. Some of the target atoms penetrate through the ion�s electron cloud causing quantum exclusions of available states. Finally, all of these effects depend on the constantly changing ion velocity.
In order to understand historical conceptual advances, it is illustrative to show how new ideas affect the scaling of stopping powers, i.e. the relative change of stopping between ions or targets or as a function of ion energy. Shown in Figure 1- 1. are the stopping powers of various ions (H, He, C, Ni, Ag and U) in various solids (C, Al, Ni, Ag, U) over 8 decades of energy. The stopping powers range over a factor of 10,000. We shall use this figure to show how new ideas affect the scaling of these curves.
Soon after the discovery of energetic particle emission from radioactive materials, there was interest in how these corpuscles were slowed down in traversing matter. From her work in 1898-1899, Marie Curie stated the hypothesis that "les rayons alpha sont des projectiles materiels susceptibles de perdre de leur vitesse en traversant la matiere." (00a). Figure 1- 2 shows her apparatus, in which particles emitted from radium (source A) went through thin metallic films (at T) and were counted by an electrometer (P). By varying the thickness of the metallic film, she was able to find the energy loss of the particles as a function of the density of the metal. Many scientists immediately realized that since these particles could penetrate thin films, such experiments might finally unravel the secrets of the atom. Early attempts to create a particle energy loss theory were inconclusive for there was not yet an accurate proposed model of the atom.
The theoretical treatment for the scattering of two point charges was derived by J. J. Thomson in his classic book on electricity (03a), see Figure 1- 3.� Much of the traditional particle energy-loss symbolism can be traced to this book which introduced a comprehensive treatment for classical Coulombic scattering between energetic charged particles. This work, however, did not attempt to calculate actual stopping powers.
Enough experimental evidence of radioactive particle interactions with matter was collected in the next decade to make stopping power theory one of the central concerns of those attempting to develop an atomic model. In 1909 Geiger and Marsden were studying the penetration of alpha-particles through thin foils, and the spread of the trajectories after emerging from the back side. They hoped to determine the distribution of charges within the foil by the angular spread of the transmitted beam. There are conflicting histories as to who made the suggestion that they look for backscattered particles - but the subsequent startling data reversed the current thought on atomic structure. They reported that about .01% of the heavy alpha-particles were scattered back from the target, and from an analysis of the data statistics such backscattered events had to be from isolated single collisions. Two years later, Rutherford was able to demonstrate theoretically (11a) that the backscattering was indeed due to a single event, and by analyzing this and electron scattering data he was able to first calculate that the nucleus of Al atoms must have a charge of about 22 and platinum would have a charge of 138 !
J. J. Thomson, director of the prestigious Cavendish Laboratory, and Niels Bohr, a fresh post-doctoral scientist who had left the Cavendish lab for Rutherford's Manchester Laboratory, published almost simultaneously (12a,13a) an analysis of the stopping of charged particles by matter, see Figure 1- 4 . These papers illustrate much of their divergent ideas on the model of an atom. Thomson incredibly ignored in his paper the alpha-particle backscattering measurements of Geiger (09a) and the Rutherford heavy-particle scattering theory (11a) which emphasized the atomic positive charge must be concentrated within the atom. But the nuclear atom with a heavy positively-charged core was the basis of Bohr's ideas. (13a,15a).
Bohr's early work is instructive because for the first time a unified theory of stopping was attempted, and we can see in this and in similar works the essential problems of stopping theory:
� How does an energetic charged particle (a point charge) lose energy to the quantized electron plasma of a solid (inelastic energy loss)?
� How do you incorporate into this interaction simultaneous distortion of the electron plasma caused by the particle (target polarization)?
� How can you extend the point charge-plasma interaction to that for a finite moving atom in a plasma?
� How do you estimate the degree of ionization of the moving atom and describe its electrons when it is both ionized and within an electron plasma?
� How do you calculate the screened Coulomb scattering of the moving atom with each heavy target nucleus it passes?
� How do you include relativistic corrections to all of the above?
This is a brief list of the major problems encountered, and scientific interest shifts back and forth between them over the decades because of external scientific tidal forces. Examples might be (a) the development of quantal scattering in the nineteen twenties, (b) the study of nuclear fission in the thirties and forties, (c) the study of nuclear physics in the fifties, (d) the technological applications of ion implantation for material modification in the sixties, and the use of ion beams in material analysis in the seventies. This ebb and flow of interest continues because of the recurrent importance of the problem, and the difficulty of calculating the penetration of energetic atoms in solids from first principles. We briefly review some of the historical milestones in this field below.
Both Thomson and Bohr concluded that the particle�s velocity was more important than its energy, see Figure 1- 5.
One of Bohr's original conclusions was that the energy loss of ions passing through matter could be divided into two components:� nuclear stopping (energy loss to the medium's atomic positive cores) and electronic stopping (energy loss to the medium's light electrons). Bohr, in his first papers, correctly deduced that the electronic stopping would be far greater than the nuclear stopping for energetic light ions such as are emitted by radioactive sources. This conclusion was based on recoil kinematics considering only the relative masses and abundance of the target electrons and nuclei.
Bohr further introduced atomic structure into stopping theory by giving target electrons the orbit frequencies obtained from optical spectra and calculating the energy transferred to such harmonic oscillators.� He noted that the experimentally reported stopping powers for heavy atom targets indicated that many electrons in these targets must be more tightly bound than the optical data suggested. He also realized that his accounting of the energy loss process was seriously limited by a lack of knowledge of the charge state of the ion inside the matter, i.e., its effective charge in its interaction with the target medium.
 |
| Figure 6 |
A major advance in understanding stopping powers came 20 years later when Bethe (30a,32a,34a) and Bloch (33a,33b) restated the problems from the perspective of quantum mechanics, and derived in the Born approximation the fundamental equations for the stopping of very fast particles in a quantized medium, see Figure 1- 6. This theoretical approach remains the basic method for evaluating the energy loss of light particles with velocities of 10 MeV/amu - 2 GeV/amu. This restriction in velocity� is because below these velocities the ion projectile may not be fully stripped of its electrons (which is assumed by the theory), and above this velocity there are additional relativistic corrections.
In the late 1930's a renewed interest was taken in energy loss with the discovery of nuclear fission and the energetic heavy particles which resulted from nuclear disintegration, see Hahn and Strassman paper which led to their Nobel Prize (39b). Various theoretical studies were published by Bohr (40d), Lamb (40b), Knipp (41b), Teller and Fermi (40c), see Figure 1- 7 and Figure 1- 8.
The problem presented by the fission fragment data was how to treat the interaction of a partially stripped heavy ion. This is called the 'effective-charge' problem, for it was hoped that if a degree of ionization for the projectile could be estimated, then the traditional stopping power theories could be used.� Bohr suggested (40d,41a) that the ion be considered to be stripped of all electrons with velocities lower than the ion velocity, and using the Thomas Fermi atom he could show that :
Eq. 1�1:����������������������� Z1*� =� Z11/3 �V / Vo
where Z1 is the atomic number of the ion, and Z1* is its effective charge in energy loss to the target electrons, V is the ion velocity and V0 is the Bohr velocity ( � 2x108 cm/sec). Lamb (40b) considered the same problem as Bohr, and suggested a similar effective charge approximation, but based on the energy rather than the velocity of the ion's electrons.� Lamb also got a similar, but less detailed, expression for stopping power assuming Thomas-Fermi atoms. He suggested that the target electron velocity distribution would significantly alter the stopping of the fission fragment, see Figure 1- 9.
Fermi (40c) considered the same points as Lamb and Bohr, but concentrated upon evaluating the interaction of a charged particle with the dielectric plasma of a solid, and the electric polarization of the medium by the particle. This polarization of the target medium had been suggested first by Swann (38a), and Fermi was able to reduce this difficult problem to a form which could be calculated.� He showed that stopping powers were universally proportional to target density, on an equal - mass - traversed basis.
A detailed suggestion for scaling stopping powers was shown by Knipp and Teller (41b), who successfully used the effective charge concept of Bohr and Lamb to scale H stopping values to equivalent He ion stopping powers.
These theoretical studies had only limited success with the fission fragment problem, and the primary practical result was to provide scaling relationships for the heavy ion stopping and ranges. That is, it allowed for interpolation and modest extrapolation from existing data into systems with different ions/targets/energies. Basically, the dominant effects were the target material and the ion's velocity. If you knew the stopping of one ion, say a proton, at two velocities in a material, and you knew the stopping of a heavy ion in that material at one of these velocities, then its stopping at the second velocity would be a direct proportionality. This law was applicable over a wide variety of velocities and ions. In fact it became so widely used that it stimulated several papers of objections to its theoretical shortcomings (63b,72b).
 |
| Figure 9 |
During the 1950's there were fundamental papers on evaluating both the energy transfer from slow particles to quantized electron plasmas, and in the energy loss to target nuclei. The study of particle stopping in a free electron gas is the first step in calculating the energy loss of an ion to a target's electrons. This problem was evaluated in Bohr's earliest papers (13a,15a) where he considered the electrons to be charged harmonic oscillators, with orbit frequencies established by the analysis of optical data. This interaction of a particle with an electron plasma was extended to quantized plasmas and then to Thomas-Fermi atoms by Bethe (30a,32a) and Bloch (33a,33b).� An excellent review of relativistic particle (>10 MeV/amu) stopping powers was made by Ahlen (80e) and this chapter will not cover in detail this subject.� For energies above 10 MeV/amu you should consult ref. (80a).
Fermi then considered how the fast charged particle would polarize a classical electron medium of the target and hence modify the particle/plasma interaction (40c). This work was extended by Fermi and Teller (47b) to a degenerate free electron gas and they found that for slow particles the energy loss would be directly proportional to the particle's velocity.� Bohr pointed out (48a) that behind the particle there would be an oscillating wake of charge, and this was evaluated more rigorously by Bohr (48b), and by Neufeld and Ritchie (55a).� A full treatment of a charged particle penetrating a quantized electron plasma was presented at about the same time by Lindhard (54a), Neufeld and Ritchie (55a) and Fano (56c). The Lindhard approach concentrates on non-relativistic particle interactions with a free-electron gas and provides a full general treatment with the following assumptions:
� The free electron gas consists of electrons at zero temperature (single electrons are described by plane waves) on a fixed uniform positive background with overall charge neutrality.
� The initial electron gas is of constant density, which is considered to be a close approximation to the conduction electrons in metals.
� The interaction of the charged particle on the homogenous electron gas is a small perturbation.
� All particles are non-relativistic.
| Figure 10 |
The Lindhard approach is widely cited in the literature as it formed part of the first unified theory of ion penetration of solids (63a), and it has been widely used as the basis for calculating the electronic stopping of ions in matter (see, for example, 67a, 70b, 72f, 74a, 75k, 77h, 78a, 79d), see Figure 1- 10.
The energy loss to target nuclei is basically the study of screened Coulomb collisions between two colliding atoms. In the 1950's, major advances were made in the elastic energy loss of the ion to target nuclei.� Bohr summarized much of the earlier work in 1948 (48a) which used the Thomas Fermi model to estimate the screened Coulomb potential, V(r) between atoms:
Eq. 1�2:����������������������� V(r)� =� ( Z1 Z2 e2 / r ) exp (-r / a)
where Z1 and Z2 are the atomic numbers, r is their separation, and a is a "screening parameter". This screening parameter is an important concept in much of the theory which follows. It essentially increases the size of an atom by moderating the effect of the nuclear positive charge on the outer electrons because the inner electrons shield some of the nuclear charge. This screening parameter then leads to a "screening function" which is the reduction of potential at a point due to the inner electron screening. Once the screening parameter is specified, then the classical scattering and energy transfer can be calculated. Bohr argued that a reasonable approximation might be (48a):
Eq. 1�3:����������������������� a� =� a0 / (Z12/3 + Z2 2/3 ) 1/2
but this approximation was not derived.
Firsov took a more practical approach and used numerical techniques to derive the interatomic potentials of two colliding Thomas-Fermi atoms (58a,b). After finding the numeric values of the potentials as a function of the atomic separation he then fitted these potentials using the Thomas-Fermi screening length and found that the best fit was obtained with:
Eq. 1�4:����������������������� a� =� a0 / (Z11/3 + Z21/3)2/3
Another problem which received wide attention in the 1950's was the degree of ionization of the ion as it goes through materials.� As we noted before, Bohr and others suggested that one simple criterion would be to assume that ions lose electrons whose orbital velocities would be less than the ion velocity.� He suggested that the ion charge fraction, Z1* / Z1 , would be :
 |
| Figure 11 |
Eq. 1�5:����������������������� Z1* / Z1� =� V / ( V0 Z12/3 )
This relation comes from the Thomas-Fermi atom which assumes the electronic charge densities of atoms are similar with a common unit of length being proportional to Z-1/3 . The charge density is proportional to Z2 , and the total binding energy scales as Z7/3 . Therefore the binding per electron scales as Z4/3 and the electron velocities are proportional to Z2/3 . This concept is illustrated in Figure 1- 11. Lamb had proposed (40b) the electron binding energy was the important stripping criterion, while Bohr suggested it was the electron velocity.� A definitive clarification was made by Northcliffe (60c) who scaled a wide variety of experimental data by dividing each ion/target/energy experimental stopping power by the stopping power of protons in the same target and at the same velocity.� In perturbation theory this ratio should scale as (Z1*)2 where Z* is the number of electrons left on the ion.� He found a large amount of data could be accurately described using the relation:
Eq. 1�6:����������������������� 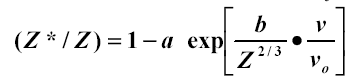
where a and b are fitting constants. The expression expands to be the Bohr relationship (assuming a = 1). By the end of the 1950's the status may be summarized as:
� A good treatment of the energy loss of a charged particle to a quantized electron plasma. The theory includes both polarization of the medium about the charge, and discussions of extensions of particle interactions with electron plasmas to electrons in atomic matter.
� A good calculation of interatomic potentials and the energy transferred during a scattering collision between two atoms.
� A good evaluation of the effective charge of heavy ions in solids for the intermediate velocity range� ( 3 v0 < v1 < 30 v0 ), where v1 is the ion velocity, and v0 is the Bohr velocity.
� How to extend the electron plasma point-charge interaction theory to the interaction with a finite sized ion?
� How to derive fundamentally the effective charge of a moving ion (where effective charge is defined as a combination of ion charge state plus target polarization)?
� And finally, how to you modify all of the above to use more realistic Hartree-Fock atoms rather than statistical atoms?
In 1963 the first unified approach to stopping and range theory was made by Lindhard, Scharff and Schiott (63a) and their approach is commonly called the LSS-theory. This work brought together all the pieces, and bridging approximations were made so that calculations of stopping and range distributions could, for the first time, be made within a single model. This remarkable achievement was the result of over a decade of study by Lindhard and collaborators (53b, 54a, 63a, 64a, 68a, 68b), with the later publications deriving in detail some of the major equations of LSS theory.� LSS theory was the peak of stopping and range theory based on statistical atoms.� With this theory it was possible to predict the range of ions in solids within a factor of two - a remarkable achievement considering it was applicable over the entire range of atomic species and energies up to the stopping power maximum (70a, 70f, 75e, 75f, 75g, 77a).� Since it was based on Thomas-Fermi atoms it was most accurate for atoms with many electrons in the intermediate range where they are neither fully stripped nor almost neutral. The theory naturally shows no shell effects.
During the 1960's and 70's the primary advances came by applying numerical methods to traditional theoretical approaches. The use of computers permitted the incorporation of more realistic Hartree-Fock atoms into the theory and gave significant improvements. These important steps were initiated by Rousseau, Chu and Powers (70b) in electronic stopping, and Wilson, Haggmark and Biersack (77c) in nuclear stopping.
One way to evaluate these theoretical steps is to estimate the accuracy with which one can calculate stopping powers. After the work by Bethe-Bloch in the 1930's, the stopping of high velocity protons could be calculated to about 20%. By the late 1950's, the excellent review article by Whaling (58c) pointed out that little could be calculated for anything heavier than a proton. This changed abruptly with the LSS theory in 1963 (63a), which created a unified approach to the stopping of low energy heavy ions. With this approach, most stopping powers could be estimated within a factor of two or three, and the ranges of these ions in single-element targets could be calculated within a factor of two.
 |
| Figure 12 |
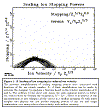
The LSS theory was the last of the comprehensive theories based on statistical models of atom-atom collisions.� Improvements in calculating stopping and ranges over the next twenty years were made by using numerical techniques and removing some of the approximations used by Bohr, Firsov and Lindhard. One new theoretical insight which has had profound implications was made by Brandt and Kitagawa (82a) where they revised the Bohr suggestion of the degree of ionization of ions traveling within solids.� Bohr had suggested that the ion's electrons which had orbital velocities less than the instantaneous velocity of the ion would be stripped off, leaving the ion only with its inner high-velocity electrons.� Brandt and Kitagawa suggested that this stripping criteria should be modified to consider the ion's electron velocity only relative to the Fermi velocity of the solid. They then proceeded to develop the formalism to allow the full evaluation of this new concept which has proved to be quite accurate. This concept is illustrated in Figure 1- 12.
Stopping powers in 2003 (the date of this chapter) can now be calculated with an average accuracy of about 5% overall, 6% for heavy ions and better than 2% for high velocity light ions.� Range distributions for amorphous elemental targets have about the same accuracy.
 |
| Figure 13 |
For extended reading in the field of the stopping and range of ions in matter, the following scientific papers are recommended. The classic review by Bohr (48a) encompasses almost everything learned in the first 50 years of study, and it is relatively easy to understand. Other reviews have been made by Whaling (58c), Fano (63b), Jackson (62a, 75a), Bichsel (70e), Sigmund (75b), Ahlen (80e), Ziegler, et al. (78a, 80a, 80b, 82b, 84a), and the International Commission on Radiation Units and Measurements (84d, 93d). For original sources, the theoretical treatment of the stopping of ions in matter is due greatly to the work of Bohr (13a, 15a, 48a), Bethe (30a, 32a, 34a), Bloch (33a, 33b), Firsov (57a, 57b, 58a, 58b) and Lindhard (53b, 54a, 63a, 64a, 68a, 68b).
1804��� Benjamin Robins, �New Principles in Gunnery�, London (1807). The only copy available in the United States is the 2nd Edition (1842) at the United States Military Academy, West Point, NY.
00a����� Mme. Pierre Curie, Comptes Rendus, 130, 76 (1900).
03a����� J. J. Thomson, "Conduction of Electricity Through Gases," Cambridge University Press, (1903).
05a����� W. H. Bragg and R. Kleeman, Phil. Mag., 10, 318 (1905).
09a����� H. Geiger and E. Marsden, Proc. Roy. Soc., 82, 495 (1909).
11a����� E. Rutherford, Phil. Mag., 21, 212 (1911); ibid, 21, 699 (1911).
12a����� J. J. Thomson, Phil. Mag., 6-23, 449 (1912).
12b����� J. Stark, Z. f. Physik, 13, 973 (1912).
12c����� C. G. Darwin, Phil. Mag., 23, 901 (1912).
13a����� N. Bohr, Phil. Mag., 25, 10 (1913).
14a����� L. Flamm, Sitzungsber, d. K. Akad. d. Wiss. Wien, Mat. -nat. Kl., 123, 1393 (1914).
15a����� N. Bohr, Phil. Mag., 30, 581 (1915).
27a����� E. Fermi, Z. f. Physik, 29, 315 (1927).
30a����� H. A. Bethe, Ann. Physik, 5, 325 (1930).
31a����� N. F. Mott, Proc. Camb. Phil. Soc., 27, 553 (1931).
32a����� H. A. Bethe, Z. f. Physik, 76, 293 (1932).
32b����� A. Sommerfeld, Z. f. Physik, 78, 283 (1932).
32c����� W. Lenz, Z. f. Physik, 77, 713 (1932); H. Jensen, Z. f. Physik, 77, 722 (1932).
32d����� C. Moller, Ann. Physik, 14, 531 (1932).
32e����� A. Sommerfeld, Z. f. Physik, 78, 283 (1932).
32f������ W. Lenz, Z. f. Physik, 77, 722 (1932).
32g����� H. Jensen, Z. f. Physik, 77, 722 (1932).
33a����� F. Bloch, Ann. Physik, 16, 287 (1933).
33b����� F. Bloch, Z. f. Physik, 81, 363 (1933).
34a����� H. A. Bethe and W. Heitler, Proc. Roy. Soc., A146, 83 (1934).
38a����� W. F. G. Swann, J. Frank. Inst., 226, 598 (1938).
39a����� E. J. Williams, Proc. Roy. Soc., 169 (1939).
39b����� O. Hahn and F. Strassman, Naturwiss., 27, 11 (1939).
40a����� L. A. Turner, Rev. Mod. Phys., 12, 1 (1940).
40b����� W. E. Lamb, Phys. Rev., 58, 696 (1940).
40c����� E. Fermi, Phys. Rev., 57, 485 (1940).
40d����� N. Bohr, Phys. Rev., 58, 654 (1940).
40e����� E. J. Williams, Phys. Rev., 58, 292 (1940).
41a����� N. Bohr, Phys. Rev., 59, 270 (1941).
41b����� J. Knipp and E. Teller, Phys. Rev., 59, 659 (1941).
41c����� J. H. M. Brunnings, J. Knipp and E. Teller, Phys. Rev. 60, 657 (1941).
47a����� G. Moliere, Z. f. Naturforschung, A2, 133 (1947).
47b����� E. Fermi and E. Teller, Phys. Rev., 72, 399 (1947).
48a����� N. Bohr, Mat. Fys. Medd. Dan. Vid. Selsk., 18, No. 8 (1948).
48b����� A. Bohr, Mat. Fys. Medd. Dan. Vid. Selsk, 24, No. 19 (1948).
49a����� P. Gombas, "Die Statistische Theorie des Atoms und hire Anwendungen," Springer-Verlag, Austria (1949).
50a����� T. Hall, Phys. Rev. 79, 504 (1950).
50b����� N. H. Marich, Proc. Cambridge Phil. Soc., 46, 356 (1950).
52a����� M. C. Walske, Phys. Rev. 88, 1283 (1952).
53a����� H. A. Bethe, Phys. Rev. 89, 1256 (1953).
53b����� J. Lindhard and M. Scharff, Mat. Fys. Medd. Kgl. Dan. Vid. Selsk., 27, No 15 (1953).
54a����� J. Lindhard, Mat. Fys. Medd. Dan. Vid. Selsk., 28, No. 8 (1954).
54b����� N. Bohr and J. Lindhard, Mat. Fys. Medd. Dan. Vid. Selsk., 28, No. 7 (1954).
63a����� J. Lindhard, M. Scharff and H. E. Schiott, Mat. Fys. Medd. Dan. Vid. Selsk., 33, No. 14 (1963).
63b����� U. Fano, Ann. Rev. Nucl. Sci., 13, 1 (1963).
63c����� L. C. Northcliffe, Ann. Rev. Nucl. Sci., 13, 67 (1963).
57a����� O. B. Firsov, Zh. Eksp. Teor. Fiz., 32, 1464 (1957).
57b����� O. B. Firsov, Zh. Eksp. Teor. Fiz.,, 33, 696 (1957).
58a����� O. B. Firsov, Zh. Eksp. Teor. Fiz., 34, 447 (1958).
58b����� O. B. Firsov, JETP,, 7, 308 (1958).
68a����� J. Lindhard, V. Nielsen and M. Scharff, Mat. Fys. Medd. Dan. Vid. Selsk., 36, No. 10 (1968).
68b����� J. Lindhard, V. Nielsen, M. Scharff and P. V. Thomsen, Mat. Fys. Medd. Dan. Vid. Selsk., 33, No. 10 (1968).
62a����� F. W. Martin and L. C. Northcliffe, Phys. Rev., 128, 1166 (1962).
63g����� J. Lindhard, V. Nielsen, M. Scharff and P. V. Thomsen, Danski Videnskab. Mat.-Fys. Medd., 33, no. 10 (1963).
64a����� J. Lindhard and A. Winther, Mat. Fys. Medd. Dan. Vid. Selsk., 34, No. 4 (1964).
63a����� J. Lindhard, M. Scharff and H. E. Schiott, Mat. Fys. Medd. Dan. Vid. Selsk., 33, No. 14 (1963).
68a����� J. Lindhard, V. Nielsen and M. Scharff, Mat. Fys. Medd. Dan. Vid. Selsk., 36, No. 10 (1968).
68b����� J. Lindhard, V. Nielsen, M. Scharff and P. V. Thomsen, Mat. Fys. Medd. Dan. Vid. Selsk., 33, No. 10 (1968).
70a����� L. C. Northcliffe and R. F. Schilling, Nucl. Data Tables, 7, 233 (1970).
70b����� C. C. Rousseau, W. K. Chu and D. Powers, Phys. Rev., A4, 1066 (1970).
70e����� H. Bichsel, Amer. Inst. of Phys. Handbook, 3rd. Ed. (1970).
70f������ W. S. Johnson and J. F. Gibbons, "Projected Range Statistics in Semiconductors," Stanford University Bookstore, Stanford, CA, 1970 (out of print).
75a����� J. D. Jackson, "Classical Electrodynamics," Chapt. 13, Wiley, New York (1962, 1975).
75b����� P. Sigmund, Chapt. 1, "Radiation Damage Processes in Materials," ed. by C. H. S. Du Puy, Noordhoff, Leyden (1975).
75e����� D. K. Brice, "Ion Implantation Range and Energy Deposition Distributions, vol. 1, High Energies," Plenum Press, New York (1975).
75f������ K. B. Winterbon, "Ion Implantation Range and Energy Deposition Distributions, vol. 2, Low Energies," Plenum Press, New York (1975).
75g����� J. F. Gibbons, W. S. Johnson and S. W. Mylroie, "Projected Range Statistics: Semiconductors and Related Materials," 2nd Edition, Halsted Press, Stroudsbury, PA, USA (1975).
77a����� H. H. Andersen and J. F. Ziegler, "Hydrogen Stopping Powers and Ranges in All Elements,", vol. 3 of series "Stopping and Ranges of Ions in Matter," Pergamon Press, New York (1977).
77c����� W. D. Wilson, L. G. Haggmark and J. P. Biersack, Phys. Rev., 15B, 2458 (1977).
78a����� J. F. Ziegler, "Helium Stopping Powers and Ranges in All Elements," vol. 4of series "Stopping and Ranges of Ions in Matter," Pergamon Press, New York (1978).
80a����� J. F. Ziegler, "Handbook of Stopping Cross Sections for Energetic Ions in All Elements," vol. 5of series "Stopping and Ranges of Ions in Matter," Pergamon Press, New York (1980).
80b����� U. Littmark and J. F. Ziegler, "Handbook of Range Distributions for Energetic Ions in All Elements," vol. 6of series "Stopping and Ranges of Ions in Matter," Pergamon Press, New York (1980).
80e����� S. P. Ahlen, Rev. Mod. Phys., 52, 121 (1980).
82b����� J. P. Biersack and J. F. Ziegler, "Ion Implantation Techniques," Springer-Verlag, p. 122 (1982).
84a����� J. F. Ziegler, J. P, Biersack, U. Littmark, "The Stopping and Range of Ions in Solids," vol. 1 of series "Stopping and Ranges of Ions in Matter," Pergamon Press, New York (1984).
84d����� M. J. Berger et al., �Stopping Powers and Electrons and Positrons�, ICRU-37, International Commission on Radiation Units, Bethesda, MD, USA (1984).
93d����� M. J. Berger et al., �Stopping Powers and Ranges for Protons and Alpha Particles�, ICRU-49, International Commission on Radiation Units, Bethesda, MD, USA (1993).